数学名词解释
- 数学线索,是从猜想到定理再到应用的过程。
- 数学命题:规律性的描述。
- 猜想:没有被证明的命题,例,哥德巴赫猜想。
- 证明:有理有据得出结论。
数学和自然科学
数学推理世界和真实测量世界的区别:
- 测量会出错,但推理不会
- 测量会有误差
- 早期文明发现了勾三股四现象,没有发现定理。
- 用事实证实和用逻辑证实的区别:
- 几乎所有自然科学定律和理论,不仅存在一个被推翻的可能性,而且有很多例外。
- 数学不能用实验来证明猜想/假说,只能从逻辑出发,通过归纳或演绎得出。
- 必须完全正确,没有例外
- 科学结论相对性vs数学结论绝对性
- 因为数学定理是基石,不能有一点缺陷
- e.g.勾股定理,在平面计算距离的方法→三角学→笛卡尔的解析几何→微积分……
看不见的缝隙
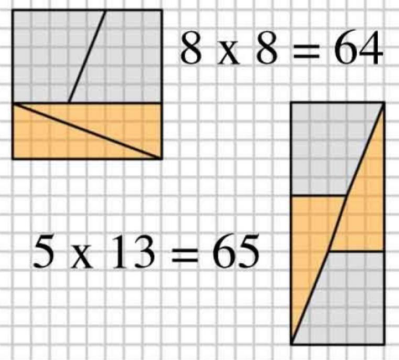
一个图形切分后,重新拼接出来的面积比原有面积大。为什么出现了看不见的缝隙?因为很多时候我们用眼睛去看,去观测,但是没有考虑到视觉和大脑作用的局限性。
a、b两人参加冥想练习,老师说用你的舌头顶部触摸上颚。a专注于老师的指令,舌头挺着坚持不了几分钟就觉得非常酸痛,这个姿势太消耗了,还怎么去冥想啊?a请教b,b说你试试闭嘴,闭着嘴的时候舌头的自然状态就是这个动作。
我们习惯用眼睛去观测,用耳朵去倾听,我们有时太眼见为实,以为自己看到的和听到的就是真实的世界,而忽略了自己身体和感觉会有局限性。
这个拼图游戏,就像瑜伽练习,刚开始看到一个倒立的姿势,感觉自己怎么可能做到,但是坚持几个月或几年后做到了。我们身体是不是也有看不见的缝隙,我们是否对自己身体能力潜力的极限有些误判?
数学和讲话
疫情是谣言的孵化器,传染病后谣言种类一般有3种:
- 阴谋论
- 有关治疗特效方法
- 对疫情的错误报道
谣言的滋生以及为何传播得快?为什么人们会觉得法国人浪漫,类似这样的模式化形象?在接受信息的时候,见到信了,还是有个“等一等”的推理过程?
- 等一等(这些消息从哪儿来?)
- 等一等(你为什么会这样认为?)
- 等一等(你为什么觉得这个不好?) ……


